John Anderson and John Davis Answer Your Neurofeedback Questions

John Davis
18 hours ago
11 min read

From Clean Signals to Lasting Skills: A Simple Guide to Filters, and Conditioning

Neurofeedback combines precise signal measurement with human learning.

Modern neurofeedback rests on two intertwined foundations. First is signal fidelity: since Hans Berger’s early EEG recordings in the 1920s, engineers and clinicians have refined amplification, electrode placement, and filtering to reliably measure microvolt-level cortical rhythms (Fisch, 1999).

Second is learning theory: mid-20th-century behavior science established how operant reinforcement, classical (respondent) conditioning, planned generalization, and metacognition shape durable behavior change, which neurofeedback leverages to help people discover and reproduce useful brain states in daily life (Skinner, 1953; Stokes & Baer, 1977).

This post is part of a series designed to explain concepts that beginners find challenging.

Filters

What do filters do?

As Fisch (1999) explains:

Filters are used to exclude waveforms of relatively high or low frequency from the EEG so that waveforms in the most important range (1-30 Hz) can be recorded clearly and without distortion. The filters receive the EEG signal after it has passed from the differential amplifier to a second, single-ended, amplifier. After passing through each filter the signal is amplified again by single-ended amplifiers (p. 46).

Neurofeedback uses several common types of filters. A high-pass filter allows frequencies higher than its cutoff point (such as 1 or 2 Hz) to pass through.

A low-pass filter allows frequencies below its cutoff point (such as 30 Hz or higher) to pass through.

A notch filter blocks frequencies around 60 Hz (or 50 Hz outside North America) to prevent electrical interference from power lines from messing up the EEG signal.

Band-pass filters allow practitioners to select a specific frequency range—for instance, 4 to 8 Hz—to define and measure a particular EEG band, such as theta waves.

When the signal requires more amplification, digital filters convert it from an analog (time-based) to a digital (frequency-based) format. Digital filters are essential for transforming the brain’s raw electrical activity into meaningful information for analysis or feedback. Each major filter type has a distinct way of shaping and interpreting EEG signals. Choosing among them involves balancing accuracy, speed, and phase integrity. Graphic © Fouad A. Saad/Shutterstock.com shows the digital reconstruction of an analog waveform.

These filters are categorized into three main types: FIR (finite impulse response), IIR (infinite impulse response), and FFT (fast Fourier transform). Most practitioners use IIR or FFT filters because they better preserve timing information.

FIR Filters

FIR filters produce outputs that fade completely after a brief impulse, depending only on current and past input values. They act like weighted moving averages and are always stable because no feedback loop is used. Their main advantage is a linear phase response, where all frequencies are delayed equally, thereby preserving the waveform shape. This makes FIR filters ideal when timing and phase relationships matter, as in event-related potentials or precise EEG analysis. The trade-off is higher computational demand and longer latency, especially at high filter orders.

IIR Filters

IIR filters, in contrast, feed part of their output back into the input, creating a theoretically infinite response. This feedback allows them to achieve sharp cutoffs with far fewer calculations, making them efficient for real-time use. However, their feedback structure introduces nonlinear phase distortion, shifting different frequencies by slightly different amounts in time. For most neurofeedback applications, where the focus is on band amplitude rather than precise waveform alignment, IIR filters are preferred because they minimize delay and maintain feedback as nearly instantaneous as possible.

Three FIR IIR Filter Questions Are FIR “better” than IIR for preserving phase relationships?

For absolute phase: Yes (FIR, linear‑phase). For relative phase/coherence between channels with matched filters: No meaningful difference.

Do IIR filters mess up coherence/phase neurofeedback?

No, provided filters are identical, time-invariant, and well-implemented, time-invariant pipelines offer low latency. Simply, issues mainly stem from transients, mismatches, or unaccounted delays.

Are IIR filters good enough for coherence neurofeedback?

Yes. They are widely used in real‑time pipelines because of low latency; just calibrate and report delays.

Filter Precision is Determined by Their Order

The precision with which IIR and FIR digital filters operate to measure a frequency is determined by their so-called order. The order setting of the filter is simply the number of samples used in the calculation of the output. Samples reflect the sampling rate of the amplifier, which is the number of times the amplifier measures or ‘samples’ the incoming EEG signal. Thus, a higher-order filter uses more samples for calculation, resulting in greater precision.

The Trade-off Between Precision and Speed

However, this precision comes at the expense of speed. A higher-order filter, using more samples (measurements), is also slower to produce an output. For example, a typical 3rd order IIR filter, often used for neurofeedback training, produces an output to the display in 11 ms when the amplifier is sampling the EEG signal at 256 samples per second (sps).

This is fast enough to provide timely feedback to the client so that the changes in the feedback display closely mirror the actual brain-based behavior being measured (sampled). A third-order filter will also accurately represent EEG activity, providing useful information for the feedback display.

When choosing a filter for offline processing of the EEG, where greater precision is desired, a higher-order filter may be used because real-time feedback is not required. Thus, the increased complexity of the calculation with a higher-order filter gives a more precise measurement.

FFT Filters

FFT filters work differently. The fast Fourier transform isn't a filter design but a mathematical algorithm that decomposes time-domain signals into their frequency components. It allows rapid computation of how much power each frequency contributes over short time windows. In neurofeedback, FFT-based processing is widely used to estimate spectral power (e.g., theta, alpha, or beta) in near real-time.

The window length determines how quickly feedback updates: shorter windows provide faster feedback but coarser frequency resolution. FFT filters can vary in complexity, mainly based on the time window chosen for analysis. A Fourier Transform calculation needs at least 1 second of data to work. Most FFT calculations use 2 seconds or more to be more precise.

More complex FFT calculations utilize a technique known as sliding windows. Think of it like taking overlapping snapshots of data—each new window includes some data from the previous one as it "slides" along the data stream. Some people mistakenly think this sliding window approach can produce output as quickly as digital filters (IIR or FIR filters). But this isn't true. No matter how often the window recalculates the data—that is, how quickly it slides along—the math behind FFT still requires at least 1 second of data to create an output.

This creates a problem for neurofeedback training: the data sent to the feedback display is too slow. For effective training, the maximum delay between when something happens in the brain and when the client sees it on the display should be 250-350 milliseconds (Cooper, Heron, & Howard, 2007; Felsinger & Gladstone, 1947; Grice, 1948; Malott & Trojan-Suarez, 2004; Miller, 2006; Miltenberger, 2008). That's about ¼ of a second.

Because of this delay, FFT is better suited for offline data processing, database comparisons, and other tasks—but it's not considered fast enough for neurofeedback training. The one exception is when training slow frequencies below approximately 10 Hz, where the FFT's slower response might be acceptable, although it's still not ideal.

Remember that all filters only reduce (attenuate, not eliminate) frequencies outside their set boundaries—for example, frequencies outside an 8 to 10 Hz range. While higher-order filters can cut off unwanted frequencies more sharply, they require longer calculation times. Additionally, when using digital filters for multiple frequencies, they must all be of the same type (such as all FFT).

There's one exception to this same-type rule: You can use different calculation types for the same neurofeedback display. For example, you might use 3rd-order IIR filters to provide direct feedback for 4-8 Hz and 15-18 Hz activity in an inhibit/reward display, while also showing the theta/beta power ratio from FFTs for informational purposes.

Filter Comparison

In practice, FIR filters preserve waveform fidelity, IIR filters enable fast and efficient feedback, and FFT filters provide flexible, frequency-based monitoring. Each has its place in neurofeedback: FIR when precision and phase accuracy are critical, IIR when immediacy is crucial, and FFT when spectral tracking is the primary goal. The key principle is consistency—using the same filter type and parameters across sessions ensures that any observed change reflects the brain, not the math.

The accuracy of IIR and FIR digital filters depends on their "order"—basically, how complex their calculations are. Higher numbers mean more complex calculations and more precise measurements. FFT filters also vary in complexity. Remember that filters only reduce (not eliminate) frequencies outside their boundaries—for example, frequencies outside an 8 to 10 Hz range.

While higher-order filters can cut off unwanted frequencies more sharply, they require longer processing times. Additionally, when using digital filters for multiple frequencies, they must all be of the same type (e.g., all FFT).

Phase Distortion and Latency

In neurofeedback, two technical considerations are particularly relevant: phase distortion and latency.

Phase distortion occurs when a filter delays different frequencies by unequal amounts, subtly shifting parts of the EEG waveform in time. This alters the true timing relationship between components of the signal.

Latency refers to the total time delay between when brain activity occurs and when feedback about it is presented to the client.

In neurofeedback, both factors matter because learning depends on the brain recognizing a clear, immediate link between its activity and the feedback it receives. Excessive phase distortion can misrepresent which brain events are being rewarded, and prolonged latency weakens the sense of cause and effect that drives operant learning. Ideally, filters and processing pipelines are designed to minimize both, preserving signal accuracy while keeping total delay short enough (usually <250 ms) for feedback to feel instantaneous and reinforce the intended neural state (Fisch, 1999).

FIR filters are typically linear-phase (phase relationships are preserved), but they may require higher-order filters, which can add computational delay. In contrast, IIR filters achieve sharp transitions with fewer coefficients but introduce frequency-dependent phase shifts (Fisch, 1999).

In feedback learning, contiguity—how immediate the feedback feels relative to neural events—modulates the effectiveness of reinforcement, allowing systems to balance the steepness of attenuation with minimal group delay.

Many platforms compute band activity using short-window FFT power or recursive IIR band envelopes. Either approach is acceptable if applied consistently across sessions, because mixing methods can complicate the interpretation of change over time.

Finally, filters attenuate but do not eliminate artifacts; good technique (e.g., posture, blink strategy, short rest breaks) is still required to maintain high signal quality upstream of the math (Fisch, 1999).

qEEG Cap Placement (precision from landmarks upward)

How should a qEEG cap be put on a client?

Electrode cap graphic © Roman Ziets/Shutterstock.com.

The electrodes in an EEG cap must follow standard 10-20 or 10-10 system placements. 10-20 system graphic adapted from Fisch (1999).

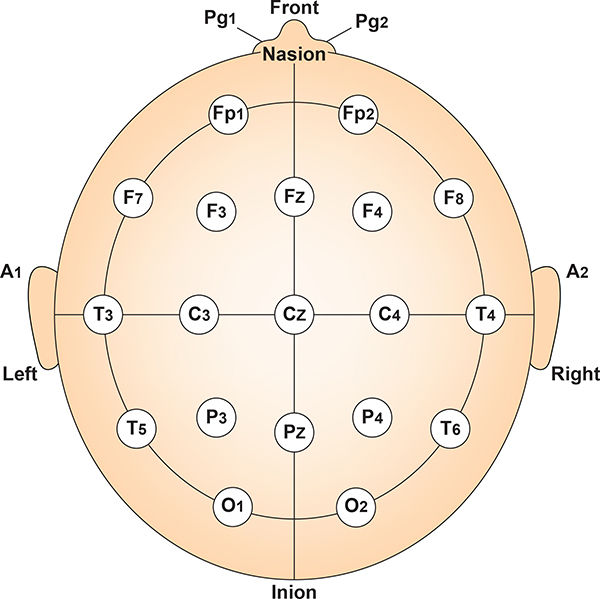
10-10 system graphic adapted from Fisch (1999).

Here's how to do it right: First, choose a cap that fits snugly but isn't too tight. Once it's on, measure where the electrodes sit compared to key bone landmarks—the nasion (bridge of nose), inion (bump at the back of the skull), and preauricular notch (the dip just in front of each ear). Then, adjust the cap so that the electrodes at positions Fp1, Fp2, T3, T4, O1, and O2 are at the correct distance from these landmarks.

The International 10–20 System remains the anchor for reproducible recordings; contemporary nomenclature often labels T3/T4 as T7/T8, but the proportional distances are unchanged. For denser coverage (10–10 or 5% systems), apply the same landmark logic at finer increments to improve spatial sampling for qEEG. Consistent placement stabilizes spectral features, improving longitudinal comparisons and topographic mapping (Acharya, Hani, Cheek, Thirumala, & Tsuchida, 2016).

Key Takeaways

Neurofeedback relies on clean signals and fast, faithful processing; the choice of filter (FIR/IIR/FFT), order, and sampling rate shapes both accuracy and delay.

For real-time training, low overall latency and minimal phase distortion preserve the brain–feedback link that enables learning; consistency across sessions prevents “math, not mind” effects.

Precise 10–20/10–10 placement anchored to cranial landmarks stabilizes topography and supports valid longitudinal/qEEG comparisons.

Glossary

amygdala: a limbic structure involved in detecting salience and mediating conditioned fear responses.

analog-to-digital conversion (ADC): a process that converts continuous voltages into discrete samples for digital analysis.

artifact: non-cerebral signal (e.g., eye blinks, muscle, movement) that contaminates the EEG.

band-pass filter: a digital/analog filter that passes only a specified frequency band and attenuates others.

beta waves: EEG activity ≈13–30 Hz associated with alert thinking and task engagement.

coherence: a frequency-specific measure of phase/amplitude coupling between

channels reflecting functional connectivity.

contingency: the reliability with which a feedback event depends on a target neural state.

delta waves: EEG activity ≈0.5–4 Hz common in deep sleep and early development.

electrode montage: a spatial arrangement/reference scheme of recording electrodes.

event-related potential (ERP): a time-locked average of the EEG to discrete events, used for precise latency/phase analysis.

Fast Fourier Transform (FFT): an algorithm that decomposes time-domain data into

frequency components; often used to estimate spectral power.

filter order: the number of coefficients/samples used to compute a filter; higher order sharpens transitions but increases computation and delay.

finite impulse response (FIR) filter: a non-recursive filter with finite response; linear phase preserves waveform shape.

frequency resolution: the ability to distinguish nearby frequencies; improves with longer analysis windows.

group delay: the effective time shift introduced by a filter; nonuniform delay across frequencies distorts phase relationships.

hippocampus: a medial temporal structure involved in context processing and generalization gradients.

high-pass filter: a filter that passes frequencies above a cutoff while attenuating slower components.

infinite impulse response (IIR) filter: a recursive filter with feedback; efficient but nonlinear phase can distort timing.

inion: the bony bump on the lower rear of the skull (external occipital protuberance) used as a landmark for EEG electrode placement.

International 10–10 system: a higher-density extension of 10–20 using finer proportional spacing. International 10–20 system: a proportional scalp mapping method using nasion, inion, and preauricular landmarks.

low-pass filter: a filter that passes frequencies below a cutoff while attenuating faster components.

notch filter: a narrowband filter that attenuates a specific frequency (e.g., 50/60 hz mains).

phase distortion: an unequal delay of different frequencies by a filter, altering true temporal relationships.

positive punishment: in operant conditioning, a process that decreases or eliminates an undesirable behavior by associating it with unwanted consequences. For example, a child's increased fidgeting dims the screen and lowers the sound.

prefrontal cortex (PFC): frontal networks supporting cognitive control, error monitoring, and metacognition.

preauricular notch: the palpable depression anterior to the ear; a 10–20 landmark.

qEEG (quantitative EEG): the statistical/spectral analysis of the EEG with topographic mapping and database comparison.

sampling rate (sps): the number of measurements per second acquired by the amplifier; sets the Nyquist limit and temporal resolution.

sensorimotor rhythm (SMR): mid-beta activity ≈12–15 Hz over central sites linked to calm, steady attention.

sliding window: overlapping spectral windows that update estimates by stepping through the time series.

spectral leakage: the energy spread across frequency bins due to windowing; reduced by tapering/longer windows.

spectral power: the magnitude of signal energy within a frequency band over time.

theta waves: EEG activity ≈4–8 Hz associated with drowsiness, memory processes, and some training protocols.

topographic map (topography): the spatial distribution of EEG features across the scalp.

ventromedial prefrontal cortex (vmPFC): a region implicated in safety learning and extinction recall.

window length: the duration of data used per spectral estimate; longer windows improve frequency resolution but increase delay.

References

Acharya, J. N., Hani, A. J., Cheek, J., Thirumala, P. D., & Tsuchida, T. N. (2016). American Clinical Neurophysiology Society Guideline 2: Guidelines for standard electrode position nomenclature. Journal of Clinical Neurophysiology, 33(4), 308–311. https://doi.org/10.1097/WNP.0000000000000316

Fisch, B. J. (1999). Fisch and Spehlmann’s EEG primer: Basic principles of digital and analog EEG (3rd ed.). Elsevier.

Milad, M. R., & Quirk, G. J. (2012). Fear extinction as a model for translational neuroscience: Ten years of progress. Annual Review of Psychology, 63, 129–151. https://doi.org/10.1146/annurev.psych.121208.131631

Morey, R. A., Dunsmoor, J. E., Haswell, C. C., Brown, V. M., McCarthy, G., & LaBar, K. S. (2015). Fear learning circuitry is biased toward generalization of fear associations in posttraumatic stress disorder. Translational Psychiatry, 5, e700. https://doi.org/10.1038/tp.2015.196

Nicholson, A. A., Rabellino, D., Densmore, M., Frewen, P., Paret, C., Kluetsch, R., … Lanius, R. A. (2017). The neurobiology of emotion regulation in PTSD: Amygdala downregulation via real‑time fMRI neurofeedback. Human Brain Mapping, 38(1), 541–560. https://doi.org/10.1002/hbm.23402

Zhao, Z., Kirlic, N., Cosgrove, K. T., Craske, M. G., Paulus, M. P., & Khalsa, S. S. (2023). Amygdala downregulation training using fMRI neurofeedback in post‑traumatic stress disorder: A randomized, double‑blind trial. Translational Psychiatry, 13, 167. https://doi.org/10.1038/s41398-023-02467-6

Zotev, V., Phillips, R., Misaki, M., Wong, C. K., Wurfel, B. E., Krueger, F., Feldner, M., & Bodurka, J. (2018). Real‑time fMRI neurofeedback training of the amygdala activity with simultaneous EEG in veterans with combat‑related PTSD. NeuroImage: Clinical, 19, 106–121. https://doi.org/10.1016/j.nicl.2018.04.010

Appreciation

John S. Anderson made significant contributions to this post's discussion of filters.

About the Author

Dr. John Raymond Davis is an adjunct lecturer in the Department of Psychiatry and Behavioural Neurosciences at McMaster University's Faculty of Health Sciences. His scholarly contributions include research on EEG changes in major depression and case studies on neurological conditions.